陶哲轩“喂饭级”AI教程来了！只用GitHub Copilot证明函数极限问题

视频新人博主陶哲轩又更新了！这次是 " 喂饭级 "AI 教程——

手把手演示如何只用 GitHub Copilot 证明函数极限问题。

（这更新频率确实 o ( ￣▽￣ ) ｄ）

据陶哲轩介绍，他此前主要将 GitHub Copilot 用于一些 " 花里胡哨 " 的代码补全，但实际情况是，如果想让它来证明数学定理，往往需要人类的 " 正确指挥 "。

因此，这一次的教学核心奔着一个目标：

让大家学会如何正确引导 GitHub Copilot。

他从定义函数极限问题出发，依次演示了求和、求差和求积定理的证明过程，以及他在过程中遇到的问题和解决方法，全程主打一个细致。

下面具体来看。

一招鲜：Copilot 代码补全 + 人工手动调整

先说结论，和陶哲轩一直以来的观念一致，GitHub Copilot 等 AI 目前在数学定理证明中仍主要用于 " 打辅 "。

Copilot 能快速生成代码框架和常见模式，对初学者尤其有用，还能提示使用已有库函数。

但面对复杂的数学细节、特殊情况和需要创造性解决方案的问题时，Copilot 的可靠性下降，需要大量人工干预和调整。

在他看来，复杂问题可能需要结合纸笔推导，确保思路正确后再进行形式化验证。

以下为得出结论的详细过程。

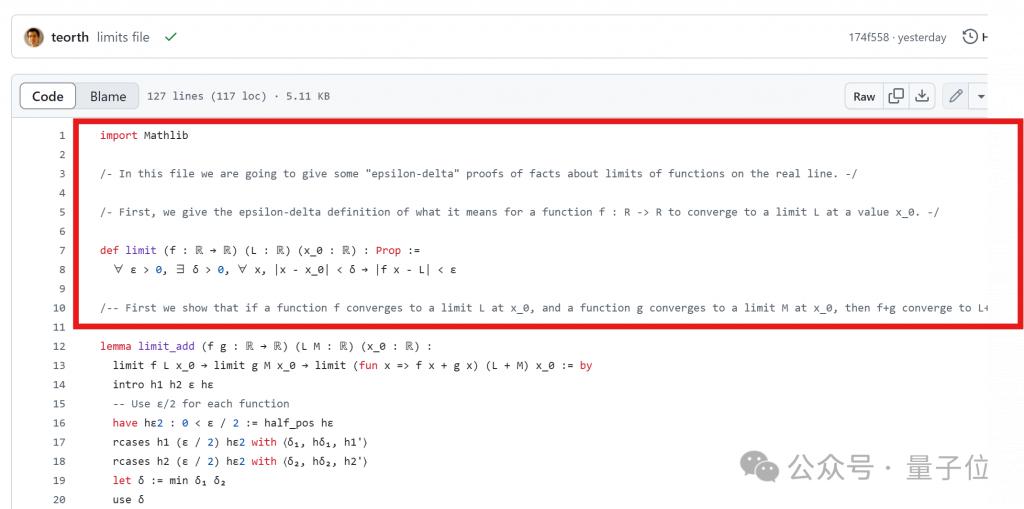
首先，他定义了函数极限问题，即 " 设 f 是从实数到实数的函数，当 x 趋近于 x_ 时 f ( x ) 收敛于 L"。

Copilot 帮忙自动补全了这个极限的 ε - δ 定义，不过由于他更喜欢用绝对值符号来表达极限的定义，所以自己又稍微修改了一下。

求和定理证明

然后他提出了第一个想要证明的问题——函数极限的求和定理证明。

如果函数 f 在 x_ 处收敛于 L，函数 g 在 x_ 处收敛于 M，那么 f+g 在 x_ 处收敛于 L+M。

Copilot 给出了正确的命题表述。

随后在证明过程中，陶哲轩用到了大量"Copilot 代码补全 + 人工手动调整 "这一模式。

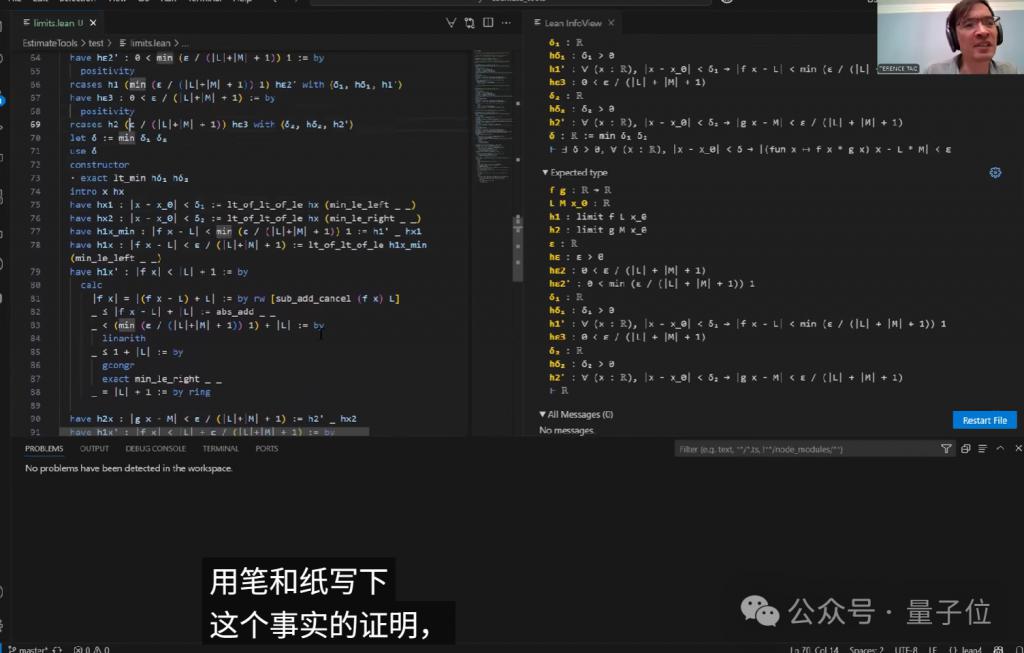
比如证明的起始步骤是提取 f 和 g 收敛的 ε - δ 条件。这里需要特别注意 δ 的选取，即取 δ ₁和 δ ₂的最小值，以保证两个函数的收敛性同时成立。

但 Copilot 最初给出的证明方式有些问题，特别是在处理 δ 的正性验证（某个数学命题或结论是否为正 ) 时不够严谨。

同时在证明不等式部分，陶使用了计算块（calc block）来构建不等式链。虽然 Copilot 自动生成了基本结构，但在绝对值符号处理和最终步骤上出现了偏差。

这里需要手动修正几个关键点：

移除了多余的绝对值符号

修正了三角不等式的应用

调整了最终表达式

另外，为了应对数学分析中合并估计值时常遇到的 ε 损失问题，陶也尝试让 Copilot 采用标准解决方法（从一开始就使用 ε /2 来进行论证），结果发现其生成的代码中 ε 仍然是原来的两倍，因此需要手动调整参数。

整体而言，他不断在 Copilot 的自动补全和手动调整之间切换。这说明 Copilot 虽然能快速生成代码框架，但关键的数学细节和严谨性仍需要人工把控。

不过值得一提的是，Copilot 在后期提示可以使用 Lean 内置的 add_sub_add_comm 引理，以简化重组步骤。

这意味着，Copilot 不仅能补全代码，还能提醒开发者利用现有的库函数。

求差定理证明

在证明了和的极限后，陶尝试用类似方法证明差的极限。

和前面一样，Copilot 能够生成基本正确的命题表述，并自动沿用了之前的证明框架。

不过在关键的一行还是出现了问题：它错误地使用了一个不存在的 sub_sub_anc 方法。

虽然陶尝试通过提示让它修正，但 Copilot 似乎无法记住上下文，给出的解决方案也不理想。

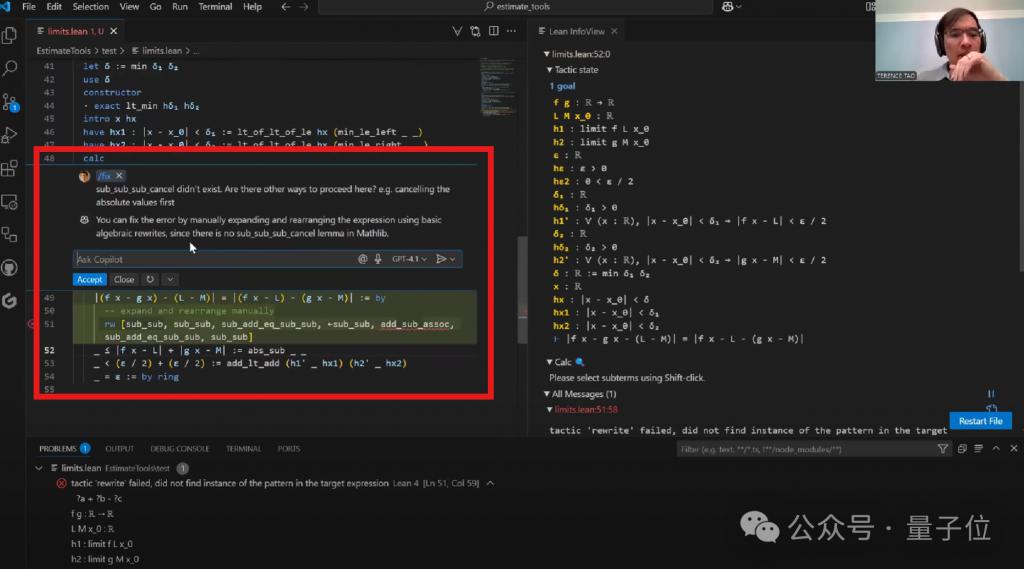
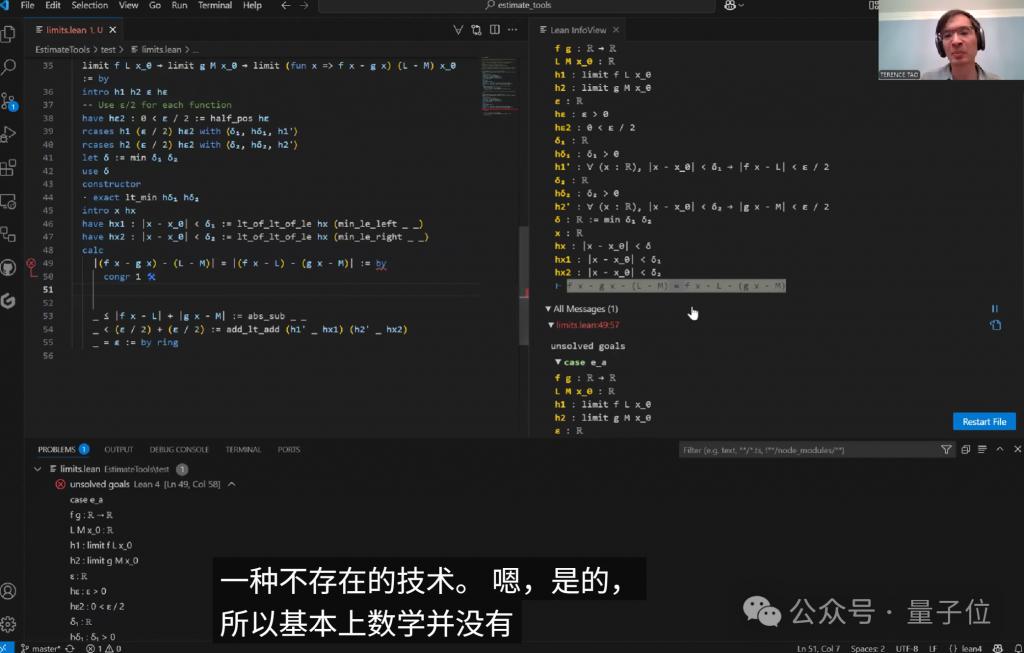
同时在处理代数表达式时，陶原本希望使用 congruence 策略来匹配等式两边，但这个策略过于激进，把问题过于简化了。

Copilot 在这个环节表现得不太稳定，有时会虚构不存在的方法。

最后陶不得不手动完成这个代数恒等式的证明，因为虽然这个恒等式在所有交换群中都成立，但 Lean 的数学库中并没有现成的直接解决方案。

求积定理证明

最后，对于函数乘积极限定理证明，陶给 Copilot 的打分为B+。

总体而言，它完成了大部分工作，但在处理 ε 的分配和绝对值不等式时出现了混乱。

首先，对于乘积极限的证明，Copilot 提出的策略是：

将 f 的近似误差设为 ε / ( 2|M|+1 )

将 g 的近似误差设为 ε / ( 2|L|+1 )

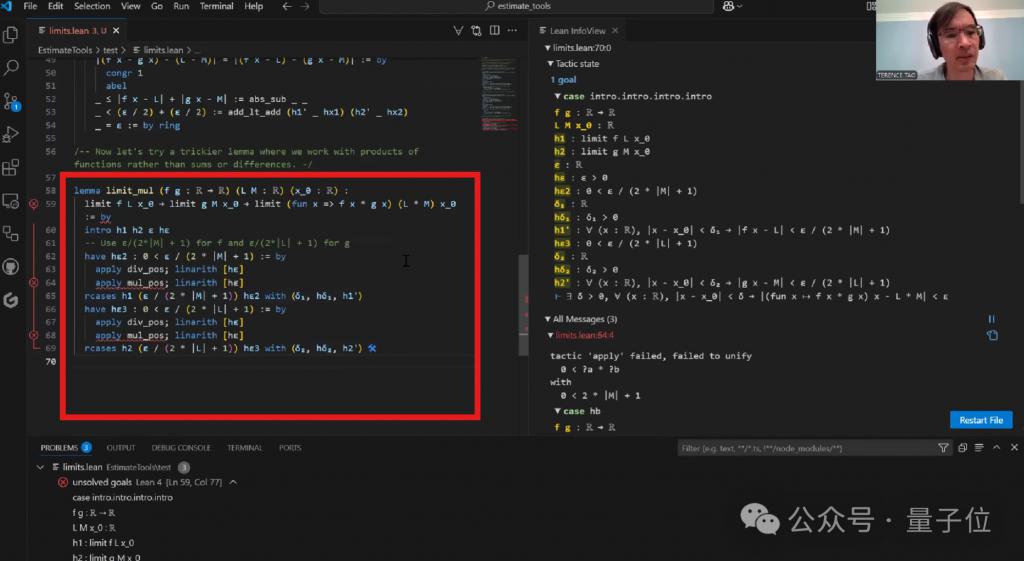
陶哲轩表示，这个思路基本正确，但在具体实现时出现了几个问题：

其一，在验证正性条件时，Copilot 试图使用多个特定引理，但实际上可以使用更通用的正性验证方法。（陶手动调整了这个部分）

其二，在处理绝对值不等式时，Copilot 错误地使用了 add_lt_add 方法，这个方法要求两边都是严格不等式，但实际情况中有一个等式。陶尝试让 Copilot 修正这个问题，但它给出的解决方案并不理想。

与此同时，在最终证明的以下几个关键步骤中，虽然 Copilot 在整体框架上提供了很大帮助，但在处理这些精细的数学细节时，还是需要人工干预来确保准确性。

使用三角不等式分解表达式

分别控制 f ( x ) -L 和 g ( x ) -M 的项

处理交叉项 L ( g ( x ) -M ) 和 M ( f ( x ) -L )

陶哲轩强调，尤其在处理不等式和绝对值运算时，需要特别注意每个步骤的适用条件。

比如在最后阶段遇到的一个 bug：Copilot 生成的代码假设 M 是正数，而实际上并没有这个前提条件。

对于这个问题，陶最后也花了一番功夫手动调整。并且他意识到，当问题复杂度达到一定程度时，Copilot 确实会变得不太可靠。

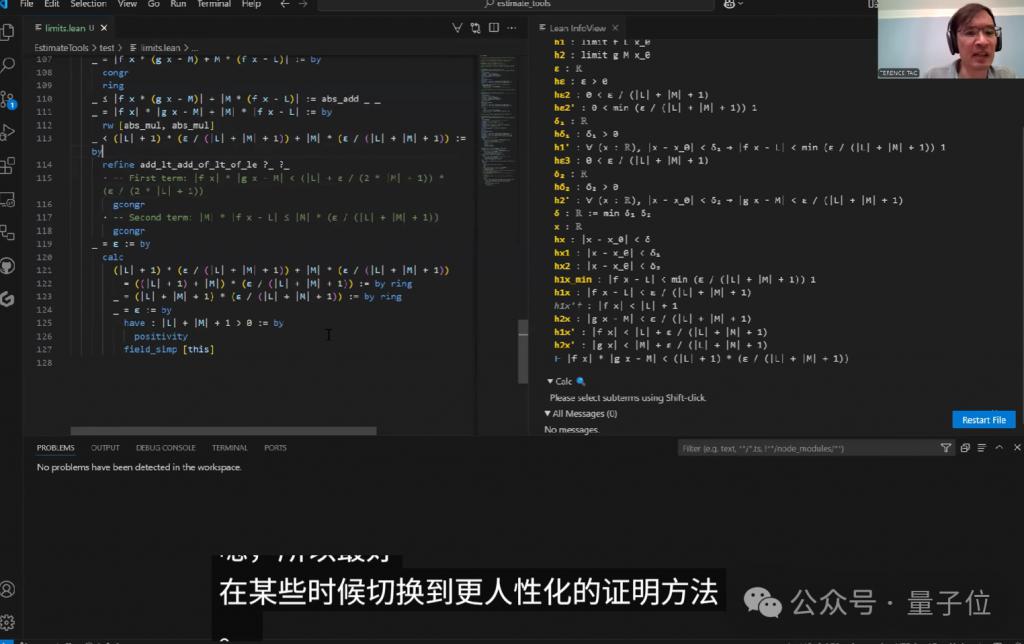
最后他得出结论，面临上述情况，切换到更传统的人工证明方法可能更有效。

如果我能先用纸笔写下完整的证明思路，确保所有 ε 参数都正确设置，然后再进行形式化验证，效率会更高。

小结一下，Copilot 这类工具在起步阶段确实很有帮助，但关键在于要懂得何时使用它，何时需要切换回传统方法。

One More Thing

以上教学收获一片好评的同时，网友的关注点也开始逐渐跑偏——

众人在线求更换录音设备。

看来油管新人博主的业务还需要精进（doge）。

参考链接：

[ 1 ] https://www.youtube.com/watch?v=c1ixXMtmfS8

[ 2 ] https://github.com/teorth/estimate_tools/blob/master/EstimateTools/test/limits.lean

—  完  —

 量子位 AI 主题策划正在征集中！欢迎参与专题365 行 AI 落地方案，一千零一个 AI 应用，或与我们分享你在寻找的 AI 产品，或发现的AI 新动向。

也欢迎你加入量子位每日 AI 交流群，一起来畅聊 AI 吧～

一键关注 点亮星标

科技前沿进展每日见

一键三连「点赞」「转发」「小心心」

欢迎在评论区留下你的想法！